PENERAPAN MODEL PEMBELAJARAN PROBLEM BASED LEARNING UNTUK MENINGKATKAN KEAKTIFAN DAN KEMAMPUAN PEMECAHAN MASALAH MATEMATIKA SISWA KELAS XI SMAN 1 SEMARANG

Edisi: Vol. 3 No. 1 September - Desember 2022

Oleh:  Agus Priyanto, S. Pd. 
(Guru SMA Negeri 1 Semarang - Jawa Tengah)

National Council of Teachers of Mathematics atau NCTM (2000:3) menyatakan bahwa standar matematika sekolah haruslah meliputi standar isi dan standar proses. Standar proses meliputi pemecahan masalah, penalaran dan pembuktian, keterkaitan, komunikasi, dan representasi. Dengan demikian proses pembelajaran matematika di sekolah diharapkan mampu meningkatkan kemampuan pemecahan masalah matematika siswa. Kemampuan pemecahan masalah yang dimaksud adalah kemampuan pemecahan masalah berdasarkan langkah-langkah Polya yang meliputi: (1) memahami masalah; (2) menyusun rencana pemecahan masalah; (3) melaksanakan rencana pemecahan masalah, dan (4) memeriksa kembali prosedur dan hasil pemecahan masalah.

Permasalahan Pembelajaran Matematika

Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan mengembangkan daya pikir manusia. Untuk itu, matematika menjadi salah satu mata pelajaran yang sangat penting untuk diajarkan kepada anak didik.

Standar proses meliputi pemecahan masalah, penalaran dan pembuktian, keterkaitan, komunikasi, dan representasi. Glenn E. Snellbecker (1974:468) mengungkapkan “problem solving involves making use of the concepts and rules which have been learned and generating new concept or rules so as to define a problem and find its solution”. Menurut pendapat tersebut, maka yang dimaksud dengan pemecahan masalah adalah suatu upaya untuk memahami permasalahan dan menemukan solusinya dengan menggunakan konsep yang telah dipelajari sebelumnya. Sumarmo (dalam Anna Fauziah, 2010) menyatakan bahwa pemecahan masalah merupakan hal yang sangat penting sehingga menjadi tujuan umum pengajaran matematika bahkan sebagai jantungnya matematika. 

Di lain pihak kesan matematika sebagai pelajaran yang membosankan, tidak disukai, dan sulit masih sering didengar dari siswa. Sebagaimana yang dikemukakan Ruseffendi (2006:156) bahwa terdapat banyak peserta didik yang setelah belajar matematika, tidak mampu memahami bahkan bagian yang paling sederhana sekalipun, banyak konsep yang dipahami secara keliru sehingga matematika dianggap sebagai ilmu yang sukar, ruwet, dan sulit. Mereka merasa banyak kesulitan  yang dihadapi ketika belajar matematika. Kesalahan-kesalahan yang biasa dilakukan siswa dalam menyelesaikan  soal-soal  matematika,  diantaranya  adalah kesalahan  interpretasi bahasa,  kesalahan  konsep,  kesalahan  prosedur,  dan  kesalahan  penarikan kesimpulan.

Salah satu materi yang diajarkan di Sekolah Menengah Atas adalah persamaan trigonometri, yakni salah satu materi yang sulit dipahami oleh siswa, karena siswa belum bisa memahami masalah atau sudah memahami masalah tetapi tidak mempunyai gagasan/ide untuk menyelesaikan masalah tersebut. Dari hasil observasi proses pembelajaran peneliti memperoleh informasi bahwa selama proses pembelajaran, siswa tidak mandiri untuk latihan mengerjakan soal-soal. Mereka hanya mengerjakan soal jika diperintah oleh guru, disamping itu dalam mengerjakan suatu soal siswa hanya mengacu pada langkah-langkah yang diberikan oleh guru sehingga siswa belum bisa berpikir sendiri memecahkan masalah. Hal ini menyebabkan siswa belum bisa untuk mengembangkan kemampuan berpikirnya dalam menyelesaikan masalah.

Disamping itu, aktivitas siswa dalam proses pembelajaran masih tergolong rendah. Mereka cenderung pasif untuk menerima materi pembelajaran. Hal ini mungkin terjadi dikarenakan guru hanya menggunakan metode ceramah selama proses pembelajaran, sehingga siswa tidak dituntut untuk aktif. Padahal menurut Slameto (2010:36) dalam proses mengajar belajar, guru perlu menimbulkan aktivitas siswa dalam berpikir maupun berbuat. Penerimaan pelajaran jika dengan aktivitas siswa sendiri, kesan itu tidak akan berlalu begitu saja, tetapi dipikirkan, diolah, kemudian dikeluarkan lagi dalam bentuk yang berbeda.

Berangkat dari permasalahan yang telah dipaparkan di atas, dapat disimpulkan bahwa untuk memperbaiki keadaan tersebut perlu diterapkan suatu sistem pembelajaran yang melibatkan peran aktif siswa. Salah satu model pembelajaran yang dapat melibatkan peran aktif siswa dan yang memungkinkan siswa untuk mengembangkan kemampuan berpikirnya untuk menyelesaikan masalah adalah model pembelajaran Problem Based Learning (PBL). Duch (dalam Aris Shoimin, 2014) menyatakan bahwa model pembelajaran ini bercirikan adanya permasalahan nyata sebagai konteks untuk para siswa belajar berpikir kritis dan keterampilan memecahkan masalah serta memperoleh pengetahuan. Arends (2007:  56-60) menyatakan bahwa sintaks pembelajaran berdasarkan masalah terdiri dari lima fase utama yaitu proses orientasi siswa pada masalah, mengorganisasi siswa dalam kelompok, membimbing penyelidikan individu maupun kelompok, mengembangkan dan menyajikan hasil, dan menganalisis dan mengevaluasi proses dan hasil pemecahan masalah. Dengan demikian, pembelajaran dengan pembelajaran dengan PBL ini diharapkan mampu membantu siswa untuk meningkatkan keaktifan dan kemampuan pemecahan masalah matematika siswa.

Pembelajaran Model Problem Based Learning

Problem Based Learning (PBL) merupakan salah satu model pembelajaran yang dapat membantu siswa untuk meningkatkan keterampilan yang di butuhkan pada era globalisasi saat ini. Problem Based Learning (PBL) dikembangkan untuk pertama kali oleh Profesor Howard Barrows sekitar tahun 1970-an dalam pembelajaran ilmu medis di McMaster University Canada (Amir, 2009). Model pembelajaran ini menyajikan suatu masalah yang nyata bagi siswa sebagain awal pembelajaran kemudian diselesaikan melalui penyelidikan dan diterapkan dengan menggunakan pendekatan pemecahan masalah.

Problem Based Learning (PBL) merupakan model pembelajaran yang menghadapkan siswa pada masalah dunia nyata (real world) untuk memulai pembelajaran dan merupakan salah satu model pembelajaran inovatif yang dapat memberikan kondisi belajar aktif kepada siswa. Problem Based Learning (PBL) adalah pengembangan kurikulum dalam proses pembelajaran. Dalam kurikulumnya, dirancang masalah-masalah yang menuntun siswa untuk mendapatkan pengetahuan yang penting, membuat mereka mahir dalam memecahkan masalah, dan memiliki strategi belajar sendiri serta kecakapan berpartisipasi dalam tim. Proses pembelajaranya menggunakan pendekatan yang sistemik untuk memecahkan masalah atau tantangan yang dibutuhkan dalam kehidupan sehari-hari (Amir, 2009).

Tahap-tahap pembelajaran PBL

• Tahap 1 - Orientasi siswa pada masalah, Guru menjelaskan tujuan pembelajaran, menjelaskan logistik yang diperlukan, mengajukan fenomena atau demonstrasi atau cerita untuk memunculkan masalah, serta memotivasi siswa untuk terlibat dalam aktivitas pemecahan masalah
• Tahap 2 - Mengorganisasi siswa untuk belajar. Guru membagi siswa ke dalam beberapa kelompok, membantu siswa mendefinisikan dan mengorganisasikan tugas belajar yang berhubungan dengan masalah.
• Tahap 3 - Membimbing penyelidikan individu maupun kelompok. Guru mendrong siswa untuk mengumpulkan informasi yang dibutuhkan, melaksanakan eksperimen dan penyelidikan untuk mendapatkan penjelasan dan pemecahan masalah
• Tahap 4 - Mengembangkan dan menyajikan hasil Guru membantu siswa dalam merencanakan dan menyiapkan laporan, dokumentasiatau model dan membantu mereka berbagi tugas dengan sesama temannya.
• Tahap 5 - Menganalisis dan mengevaluasi proses dan hasil pemecahan masalah Guru membantu siswa untuk melakukan refleksi atau evaluasi terhadap proses dan hasil penyelidikan yang telah dilaksanakan.

Penelitian PBL Materi Triginometri

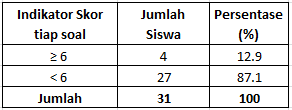
Dalam penelitian ini siswa dikatakan bisa memecahkan suatu masalah jika siswa tersebut bisa memahami dan melakukan perencanaan penyelesaian masalah dengan benar. Oleh karena itu indikator keberhasilan untuk tes kemampuan pemecahan masalah matematika adalah siswa mampu mencapai skor 6 untuk setiap soal dengan catatan bahwa skor 6 itu diperoleh dari 2 skor maksimal untuk tahap memahami masalah dan 4 skor maksimal untuk tahap melakukan perencanaan masalah dengan benar. 

Penelitian dengan menerapkan pembelajaran tipe Problem Based Learning ( PBL ) terdiri dari 2 siklus dan setiap siklus terdiri dari siklus 1 terdiri dari 4 pertemuan dan siklus 2 terdiri dari 3 pertemuan. Pada masing-masing siklus terdiri atas 4 tindakan, yaitu: perencanaan, pelaksanaan, observasi dan refleksi. Berikut adalah paparan hasil penelitian untuk masing-masing siklus.

Hasil Tes Siklus I 

Hasil tes siklus I siswa setelah penerapan pembelajaran tipe PBL  pada sub materi pokok trigonometri  dan persamaan kuadrat trigonometri adalah sebagai berikut:

Tabel. Capaian Skor Tes Siklus I

Hasil Observasi Keaktifan Siswa

Keaktifan siswa selama proses pembelajaran dapat dilihat dari hasil observasi yang dilakukan oleh peneliti terhadap selama berlangsungnya proses pembelajaran dengan PBL adalah sebagai berikut:

Tabel. Keaktifan Siswa (Siklus I)

Hasil Tes Siklus II 

Hasil tes kemampuan pemecahan masalah matematika pada siklus II setelah penerapan pembelajaran kolaboratif tipe PBL  adalah sebagai berikut:

Tabel. Capaian Skor Tes Siklus II

Hasil Observasi Keaktifan Siswa

Keaktifan siswa selama proses pembelajaran dapat dilihat dari hasil observasi yang dilakukan peneliti selama berlangsungnya proses pembelajaran dengan PBL,

Tabel. Keaktifan siswa (Siklus II)

Kemampuan Pemecahan Masalah Matematika

Kemampuan pemecahan masalah matematika siswa pada pokok bahasan trigonometri diukur melalui tes uraian di setiap akhir siklus. Peningkatan jumlah siswa yang mencapai skor 6 untuk tiap soal pada tes akhir siklus I dapat diperoleh dengan cara membandingkan dengan jumlah siswa yang mencapai skor 6 untuk tiap soal sebelum dilakukan tindakan dan setelah dilakukan tindakan siklus I. Berikut ini peningkatan jumlah siswa yang mencapai skor 6 untuk tiap soal pada siklus I. 

Tabel. Peningkatan Siswa yang Mencapai Skor 6 pada Tes Siklus II

Data diatas yang menunjukkan adanya peningkatan kemampuan pemecahan masalah matematika siswa dapat disajikan dalam bentuk diagram di bawah ini:

Diagram Kenaikan Persentase 

Kemampuan Pemecahan Masalah Matematika Siswa pada Prasiklus, Siklus I, dan Siklus II

Kesimpulan

Keaktifan siswa diukur melalui observasi langsung oleh observer selama pembelajaran matematika berlangsung. Masing-masing siswa diamati oleh dua observer dengan cara memberi tanda (√) pada lembar observasi keaktifan siswa jika siswa tersebut melakukan kegiatan yang dimaksud. Peningkatan keaktifan siswa selama proses pembelajaran pada siklus II dapat dilihat dengan cara membandingkan jumlah siswa dengan kategori keaktifan rendah, sedang, dan tinggi  pada saat proses pembelajaran siklus II. Berikut Tabel peningkatan keaktifan siswa saat siklus I dan siklus II.

Tabel. Peningkatan Kategori Keaktifan Siswa pada Siklus II

Peningkatan keaktifan siswa dari prasiklus, siklus I, dan siklus II disajikan dalam bentuk diagram  berikut

Diagram Capaian Keaktifan Siswa pada Prasiklus, Siklus I, dan Siklus II

Dengan adanya peningkatan yang terjadi di setiap tindakan dapat disimpulkan bahwa penerapan model pembelajaran kolaboratif tipe Problem Based Learning (PBL) dapat meningkatkan keaktifan dan kemampuan pemecahan masalah matematika siswa kelas XI .

DAFTAR REFERENSI

• Arikunto, Suharsimi. (2002) . Prosedur Penelitian: Suatu Pendekatan Praktek. Jakarta: PT Rineka Cipta.
• Arikunto, S., Suhardjono, & Supardi. (2007) . Penelitian Tindakan Kelas. Jakarta: Bumi Aksara.
• Budiyono. (2003) . Metodologi Penelitian Pendidikan. Surakarta: Sebelas Maret University Press.
• Fauziah, Anna. (2010) . Peningkatan Kemampuan Pemahaman dan Pemecahan Masalah Matematika Siswa SMP melalui Strategi REACT. Forum Pendidikan, 2010/Vol.30 (1), 1-13.
• Moleong, Lexy J. . (1999) . Metodologi Penelitian Kualitatif. Bandung: PT Remaja Rosdakarya Offset.
• NCTM. (2010) . Principles and Standards for School Mathematics. Reston, Virginia
• Polya, George. (1973) . How To Solve It (second edition). New Jersey: Princeton University Press.
• Russeffendi ET. (1991). Pengantar kepda Guru Mengembangkan Kompetensinya dalam Pengajaran Matematika melalui CBSA. Bandung: Tarsito.
• R.Soedjadi . (2010) . Kiat Pendidikan Matematika di Indonesia, Konstatasi Keadaan Masa Kini Menuju Harapan Masa Depan. Jakarta: Direktorat Jenderal Pendidikan Tinggi Departemen Pendidikan Nasional.
• Sanjaya, Wina. (2009) . Kurikulum dan Pembelajaran: Teori dan Praktek KTSP. Jakarta: Kencana.
• Slameto. (2010) . Belajar dan Faktor-faktor yang Mempengaruhinya. Jakarta: Rineka Cipta.
• Snellbecker, Glenn E. (1974) . Learning Theory Instructional Theory and Psychoeducational Design. New York: Me, Graww-Hill Inc.
• Sudjana, Nana. (1991) . Penilaian Hasil Proses Belajar Mengajar. Bandung: PT Remaja Rosdakarya Offset.
• Wena, Made. (2010) . Strategi Pembelajaran Inovatif Kontemporer: Suatu Tinjauan Konseptual Operasional. Jakarta; Bumi Aksara.
• Wirodikromo, Sartono. (2004) . Matematika untuk SMA kelas XI. Jakarta: Erlangga.